Learn how fractals can
turn your enterprise into an Idea Factory
Rapidly leverage patented AI solutions and transformative methodologies inspired by Fractals to reimagine how your teams work, engage with customers, and scale their best ideas with the click of a button.
What is a Fractal?
The world thinks in files. We use fractals to think in Ideas®
Introduction to Fractals:
A Fractal is a type of mathematical shape that are infinitely complex. In essence, a Fractal is a pattern that repeats forever, and every part of the Fractal, regardless of how zoomed in, or zoomed out you are, it looks very similar to the whole image.
Fractals surround us in so many different aspects of life. Since the term is becoming more widely used we wanted to create the definitive guide to understanding what Fractals are, why Fractals are important, and how Fractals impact our lives. This Ultimate Guide to Fractals will address common questions like: What is a Fractal? How do fractals work? What are Fractals used for? and much more.
The major different types of categories of Fractals we will explore in this guide include:
- Fractals in Nature
- Fractals in Computers
- Fractal Shapes
- Fractals in Math
- Fractals in 3D modeling
- Fractal in Information and Data Management
- Fractals in Computer System Architecture
- Fractals in other areas of Technology
- Fractals in Physical Structures
- Fractals and Human Psychology
- Fractals in Time
- Fractals in Sound
- Fractals in Art
- Fractals in Law
Background on Fractals:
Before we begin exploring Fractals in detail, let’s first take a look at some of the most common Fractals that you may encounter. The most commonly shown Fractal is called the Mandelbrot set, named after the mathematician Benoit Mandelbrot who coined the term Fractal. The english word Fractal comes from the latin word frāctus, which means “broken” or “fractured,” which is appropriate given that there are fractional components within each Fractal.
A shape does not have to be exactly identical to be classified as a Fractal. Instead shapes that display inherent and repeating similarities are the main requirement for being classified as a Fractal.
Here is an image representing the Mandelbrot Set Fractal one of the most iconic math fractals:

Fractals in Nature
Once the basic concept of a Fractal is understood, it is shocking to see how many unique types of Fractals exist in nature. Some of the most common examples of Fractals in nature would include branches of trees, animal circulatory systems, snowflakes, lightning and electricity, plants and leaves, geographic terrain and river systems, clouds, crystals.
Fractal Trees:
Fractals are seen in the branches of trees from the way a tree grows limbs. The main trunk of the tree is the origin point for the Fractal and each set of branches that grow off of that main trunk subsequently have their own branches that continue to grow and have branches of their own. Eventually the branches become small enough they become twigs, and these twigs will eventually grow into bigger branches and have twigs of their own. This cycle creates an “infinite” pattern of tree branches. Each branch of the tree resembles a smaller scale version of the whole shape.

Fractals in Animal Bodies
Another incredible place where Fractals are seen is in the circulatory and respiratory system of animals. If you take the human respiratory system, you will see a Fractal that begins with a single trunk (similar to the tree) that branches off and expands into a much more fine grained network of cavities.
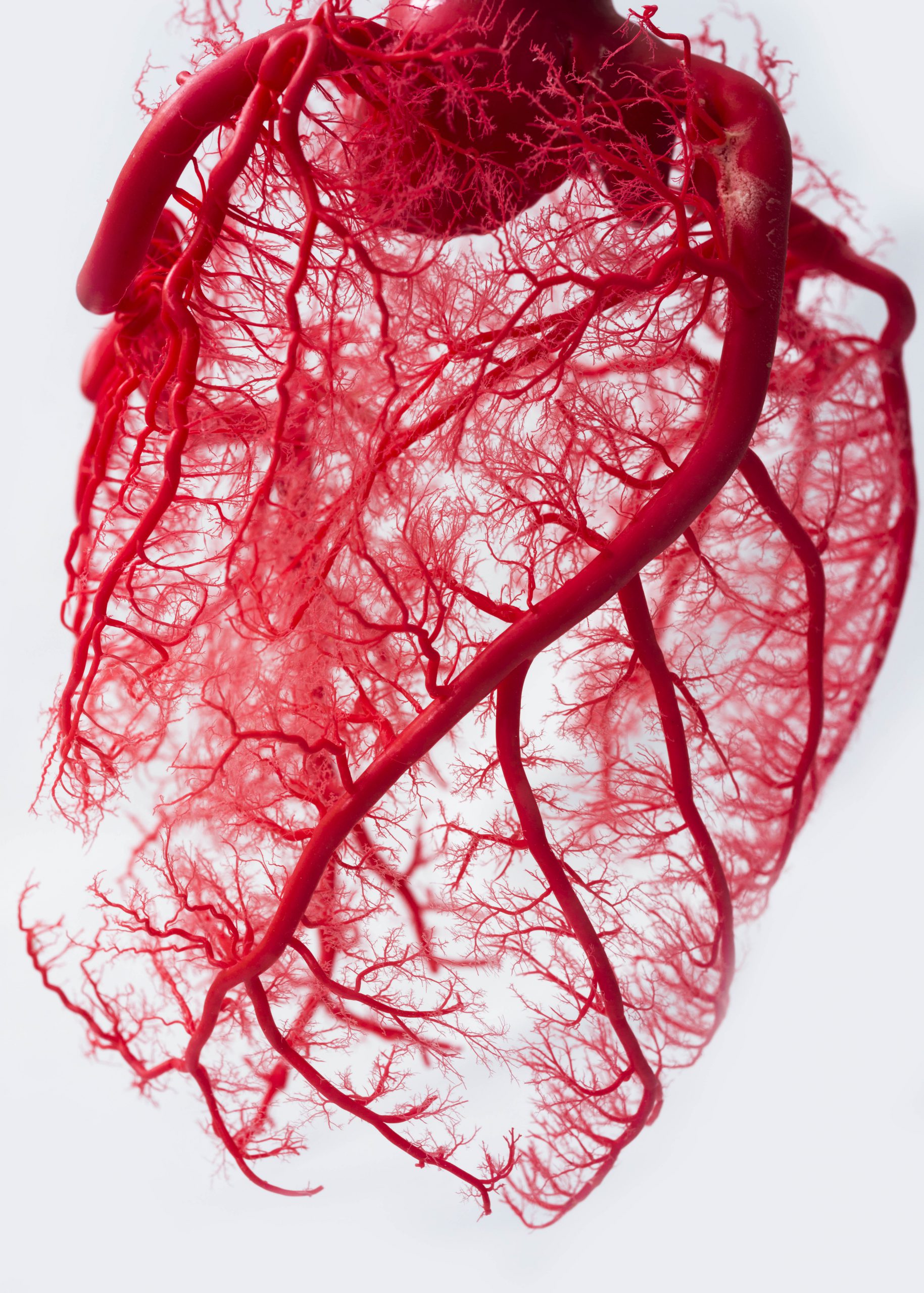
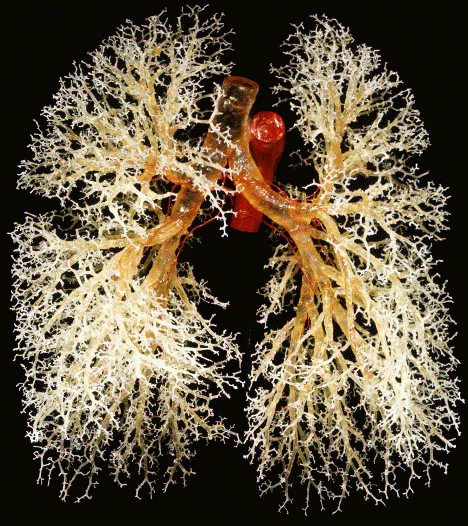
Fractal Snowflakes
We’ve all heard that every snowflake is unique and one of the contributing factors to the uniqueness of snowflakes is that they form in Fractal patterns which can allow for incredible amounts of detail and also variation. In the case of ice crystal formations, the starting point of the Fractal is in the center and the shape expands outward in all directions. As the crystal expands, the Fractal structures are formed in each direction. Just like the other examples of Fractals we have shared above, each iteration of the shape gets smaller and more detailed, which also contributes to the overall complexity of the shape.

Fractal Lightning and Electricity
If you’ve ever watched a lightning storm, you’re getting a front row show to one of nature’s most powerful displays of Fractals. When electricity passes through a medium that does not conduct electricity well (like air) the pattern that is created becomes Fractal. The reason this phenomenon forms is because of how the electricity interacts with the air. As the current passes through the air, it becomes superheated. Superheating of the air changes its electrical conductivity and allows the current to fragment out. This process repeats for each level of fragmentation and soon you get a Fractal. You’ll notice that if you invert an image of a lightning strike or electrical discharge, you’ll see great resemblance to a tree. This is because both are Fractals.


Fractals in Plants and Leaves
Next time you eat a salad, a pineapple, broccoli, or a handful of other foods, you are actually eating a Fractal! Plants and leaves, just like animals, have internal structures that distribute nutrients through a network of Fractals. These structures allow for easy distribution of liquids and other life sustaining materials to travel through the plant and support the life of every cell.
Beyond the cellular level, some types of plants themselves are very Fractal in look. One of the most notable examples is a type of broccoli called Romanesco broccoli. This type of broccoli has an incredible structure of spires which emanate from a single source (similar to the Fractal Snowflake) that in turn have their own spires which continue on to the tip of the plant.
A fern is another great example of a Fractal. Ferns are essentially made up of the same general structure repeated over and over again.


Fractals in Geography, Rivers, and Terrain
Much like Lightning, Trees, and Plants, Geography, Rivers, and Terrain also often fall under the Fractal category. If you think about how terrain is formed and weathered, a good part of the landscape can be attributed to water erosion. Similar to the networks that distribute fluids throughout an organism, rivers and other bodies of water collect, move, and distribute water throughout a landscape. A great example of this could be the journey water takes as it moves from a stream, to a river, to a lake or another large body of water.
As rivers and other bodies of water are formed, they are also carving out the geographic landscape which makes the land the bodies of water travel on Fractals as well. A great example of how Fractal geometry impacts geography comes in the form of measuring a coastline. If you measure a coastline with a mile long ruler, you will be able to get a very rough estimate as to how long the coast line is, but you will not be able to capture any of the finer detail like bumps, ridges, and outcroppings. However, if you shrink your ruler down to a yard, you are suddenly able to capture much more fine detail, because your instrument for measurement is much more precise. Each time you increase the granularity of your measurement, you are able to increase the accuracy of your measurement, which in the case of a coastline will increase the perimeter, because you will be able to capture more of those fine details. Because coastlines have Fractal geometry, the detail is extremely fine and will result in a very large perimeter.
Another way to think about modeling coastline geometry would be to think about the challenge of creating the outline if you are forced to use a set of cubes. To get any accurate detail the cubes must be very small, otherwise detail will be lost. You could also equate this challenge to the resolution of an image. If you have a low resolution image the pixels are very big which makes the image blurry and hard to see. As you increase the resolution of the image, the pixels get smaller, and the image becomes more detailed.



Fractals in Clouds
Clouds also display characteristics of Fractals. The turbulence that is found within the atmosphere has an interesting impact in the way water particles interact with each other. Turbulence is Fractal in nature and therefore has a direct impact on the formation and visual look of clouds.The amount of condensation, ice crystals, and precipitation expelled from the clouds all impacts the state of the cloud and the system’s structure and therefore the turbulence.


Fractals in Crystals
Like ice formations, other natural forms of crystals like those created from minerals can also exhibit Fractal properties. Depending on the specific formation of crystal and the minerals used some are more fractal in appearance than others. A great example of this would be the cubic nature of some formations of Amethyst or pyrite.


For more information on Fractals in Nature, we recommend you explore Beniot Mandelbrot’s iconic book The Fractal Geometry of Nature, which pioneered these ideas.
Fractals in Computers
While Fractals surround us in so many different ways, there are physical limitations as to how deep we can go in examining the fractals seen in the physical world. Eventually if we zoom in far enough we will see individual molecules and no longer be able to see the fractal pattern. In computers the story is a bit different. Computers have unlocked our ability to explore fractals at an incredibly detailed level, and because fractals are derived from mathematical equations, we can explore these shapes at an infinity deep level.
Beyond just the practical applications of using computers to research and build Fractals, the computer’s capability calculating incredible numbers gives us the ability to use complex Fractal equations for many different real world applications like 3D Modeling and terrain modeling where incorporating Fractal equations adds to the level of realism or accuracy of the project.

Fractals in 2D Modeling
Computers allow Fractals to be generated as mathematical formulas rather than finite shapes, the benefit of creating Fractals in this way enables a user to deeply explore the implications of Fractal equations. For example in the 1800s Karl Weierstrass a German mathematician created a fractal shape that has no flat surfaces, and instead is only corners. In traditional geometry, such action would be impossible, however using Fractals a formula can be created that has jagged corners at every scale of the object. This means that if you have a line on a shape that appears to be straight, if you were to zoom in closer, you would quickly see that “straight” line is actually covered in jagged edges. This pattern repeats infinitely, resulting in an infinite jagged shape with no straight lines, and only edges, as well as an infinite perimeter. Exploring this accomplishment in meaningful detail would not be possible without modern computers.
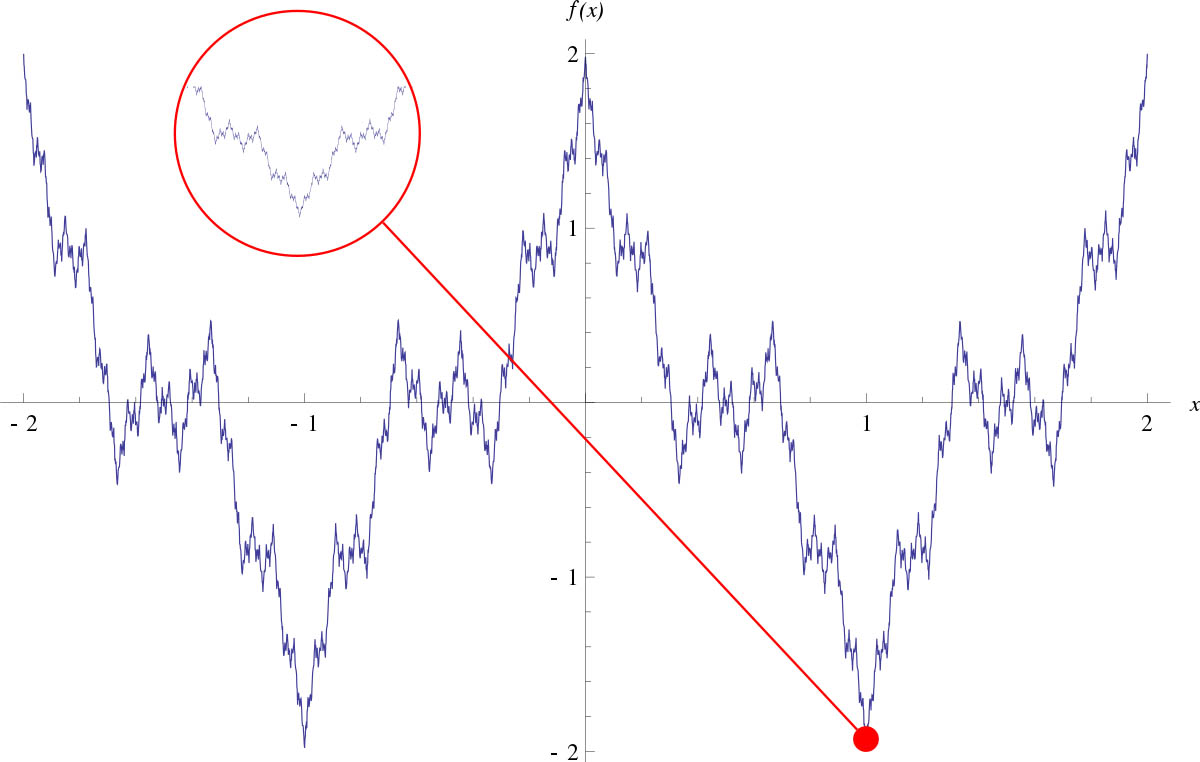
The exploration of Fractals within computers started in the 1960s when Beniot Mandelbrot worked at computing giant IBM. The massive computing power made available due to his employ at IBM allowed Mandelbrot to create and manipulate fractals with more precision than ever before. Mandelbrot’s pioneering work with Fractals was honored by naming the most iconic Fractal after his name: “The Mandelbrot Set.”
The first computer generated image of the Mandelbrot set was generated in 1980 by an IBM supercomputer. Today any computer can easily perform the calculations required to explore basic Fractals.
Fractals are displayed in computer programs by coloring the affected pixels. The colored pixels are not part of the set, and the black pixels are part of the set. In a traditional representation of a Fractal, each level of the Fractal is represented by a different color or color gradient. In the example of the mandelbrot set, Blue depicts the first level of the Fractal, with subsequent levels of the Fractal being colored yellow and moving into more red hues the deeper it goes. There is no required color scheme for Fractals, this is just one example.
As the use of computers to explore Fractals increased, a new discovery was made in the form of what is called Zoom Symmetry. Zoom Symmetry means that a shape is identical or nearly identical regardless of how zoomed in the observer is. This means that if you are looking at the entire shape, you will see almost the exact same thing even if you were to zoom in to look at a very small portion of the whole.
Thinking back to our exploration of Fractals in nature above, a great way to understand zoom symmetry is with the example of the tree branches, as you zoom into the tree, the branches retain their loose symmetry.
Fractals in Information and Data Management
Fractals have a significant impact on how we think about information and data management. If you consider the way information is organized and structured, it originates with some kind of overarching category, take this webpage as an example. The overarching category is about fractals. From there, the information is broken down into individual sub categories or topics, like fractals in Nature, fractals in Computer Systems and Fractals in Math. Each of these topics also has their own set of fragmentation into similar or related sub categories of ideas. While fractals for information are finite, you can see a similar branching tree pattern in the way the information is structured. Eventually the information will be broken down into the smallest possible modular component possible about the subject. Approaching information and organization of content using fractal theory is called the Hanby Iternal Information Theory. John Byron Hanby IV developed the Hanby Iternal Information Theory in an effort to better organize and categorize information in a systematic way that could optimize processing, management, and creation of content using the information.
In the example described above, breaking down all key points about a topic into modular components results in the creation of IdeaBlocks. In Hanby Iternal Information Theory a IdeaBlock is A IdeaBlock is any self-contained concept or idea about a topic, i.e. a company, product, service, etc. Depending on the media format a IdeaBlock is typically 2 – 3 sentences in length or 15 seconds of time.
Hanby created the IdeaFORGE® technology as a way to optimize and simplify the use and application of the Hanby Iternal Information Theory.
Applications for the Hanby Iternal Information Theory are very broad and can encompass all forms of information structure and management. Some of the most common use cases would include the management of communications between people or organizations in the corporate communications world, or in the education space, with each IdeaBlock being tailored around a specific piece of information.
Careful attention must be given to how information is fragmented to ensure Hanby Iternal Information Theory is able to be applied. The self-similarity of Fractals must be applied to the information being fragmented in order for the IdeaBlocks to be usable. For example think of the branching of trees as discussed in the Fractals in nature. The tree must start with a single unified trunk, or if there is more than one “trunk” then you are not beginning at the point of origin for the tree. The same is true for Hanby Iternal Information Theory. In order to organize information successfully, you must identify your point of origin and ensure the information categorization and fragmentation is properly componentized. For more details on the Hanby Iternal Information Theory, the IdeaFORGE, and IdeaBlocks, please contact us about the IdeaFORGE Certification Program.
Fractals in Science and Technology:
Fractals have applications in many other areas of science and technology. Some of the major applications can be found in further reading from the featured links below. Some of these links are to books available for purchase through the Amazon Affiliate program.
- Fractal antennas
- Fractal transistor
- Fractal heat exchangers
- Digital imaging and Image Compression, and Digital photographic enlargements
- Fractal Signal Compression
- Architecture (The Fractal Dimension of Architecture Book)
- Fractal Modeling of Urban growth
- Detection of Life using Fractal Analysis
- Fractal in soil mechanics
- Computer and video game design
- Fractography and fracture mechanics
- Small angle scattering theory of fractally rough systems
- Fractal Camouflage Pattern Generation, such as MARPAT
- Technical analysis of price series for Stocks, Currencies and other commodities.
- Fractals in networks
- Medicine (Fractals in Biology and Medicine Volume IV)
- Seismic Activity Study
- Search and rescue plan generation using Fractals

Fractals in Math:
Hundreds of books have been written exploring the mathematical intricacies of Fractals. This section of the Ultimate Guide to Understanding Fractals is meant to give a high level overview of some of the major mathematical concepts.
We will explore Fractals as they are represented by math formulas, the concept of dimensionality and how Fractals exhibit Fractional Dimensions, as well as how some of the most iconic Fractal shapes were created using math.
Fractal Shapes
Before we go deep into mathematic formulas, let’s first look at a few common representations of Fractals that originate from mathematic formulas. Understanding how these shapes look, and how they may differ from Fractals found in nature will be critical to concept understanding.

Just like Fractals in nature, the Fractal shapes shown in this image are self-similar and identical regardless of what scale you look at. This is most easily seen with the solid black square and triangles.
The solid Triangle is called a Sierpinski Gasket. To create a Sierpinski Gasket you will begin with a single triangle, with each iteration you will start to remove the center of the triangle. With each repetition, you will see more and more of the triangle become empty space. Also, notice how each new Triangle formed looks like the next iteration and very similar to the shape as a whole.

Another great example of a Fractal shape would be the shape known as the von Koch Snowflake. The von Koch Snowflake takes the opposite approach to the Sierpinski Gasket. Instead of subtracting triangle material, the von Koch Snowflake adds triangular material. You begin with a single triangle, with each iteration, each site of the triangle has a proportional triangle added to the side. Then each of those sides has another triangle added, and this pattern repeats infinitely. After a number of iterations you can zoom in on a section of the pattern and see the self-similarity between the edges.

Fractal Dimensions
These shapes, and all Fractals exhibit what we call Fractional Dimensions. The name “Fractal” is derived from the latin concept of Fractional and Fractured. This is in reference to the fractional dimensions. In simple forms there are three major categories of dimensions, the first is single dimension, which can be represented by a line segment only exhibiting length. The second is two dimensions which can be represented as a flat plane which only exhibits length and width. Third is 3 dimensional objects, which can be represented by a cube, where the cube has a length, a width, and a depth.
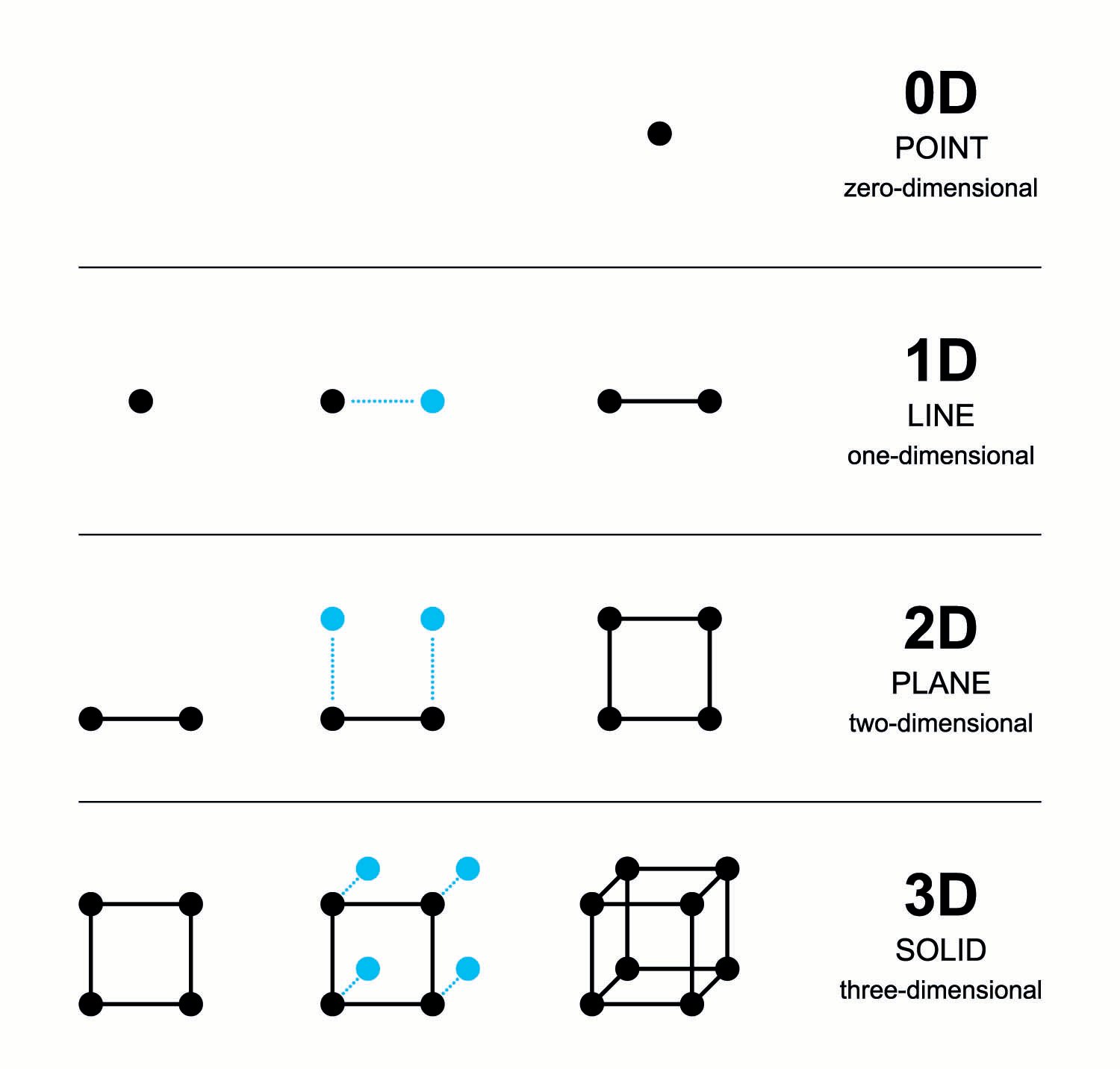
Fractals exhibit properties that differ from these major types of dimensions. Fractals can actually have fractional dimensions, like for example 2.5 dimensions.
A great way to explain dimensionality is thinking of it as a measure of roughness, or how well does a given shape fill the space around it. A sphere for example fills 3 dimensions of space because it is a solid object. A piece of paper fills 2 dimensions of space. A fractal can be somewhere in the middle. Imagine you take the 2 dimensional piece of paper and crumple it up into a ball. That ball of paper now has a length, a width, and a depth, but it is also wrinkled and has lots of voids between the crumpled layers of paper.

Because the crumpled paper ball is not completely solid, it has a fractional dimension value, likely somewhere around 2.5 (between the two dimensional flat piece of paper and the 3 dimensional solid sphere). Another great example would be human lungs, where the lungs are not perfectly smooth, they are rough and have many small cavities designed to capture oxygen.
To learn more about how to calculate Fractal Dimensions please see this article.
Creating the Mandelbrot Set Fractal
The Mandelbrot set is created by following the formula of [ zn+1 = zn^2 + c ] in this formula, c represents a point on the plane grid shown in the image. Z is a number which is squared, and when added to C will output a new Zn+1 value. If the chosen C value allows this formula to increase to infinity, then the chosen C value is not part of the mandelbrot set. If the number does not increase to infinity, then the number is part of the mandelbrot set.
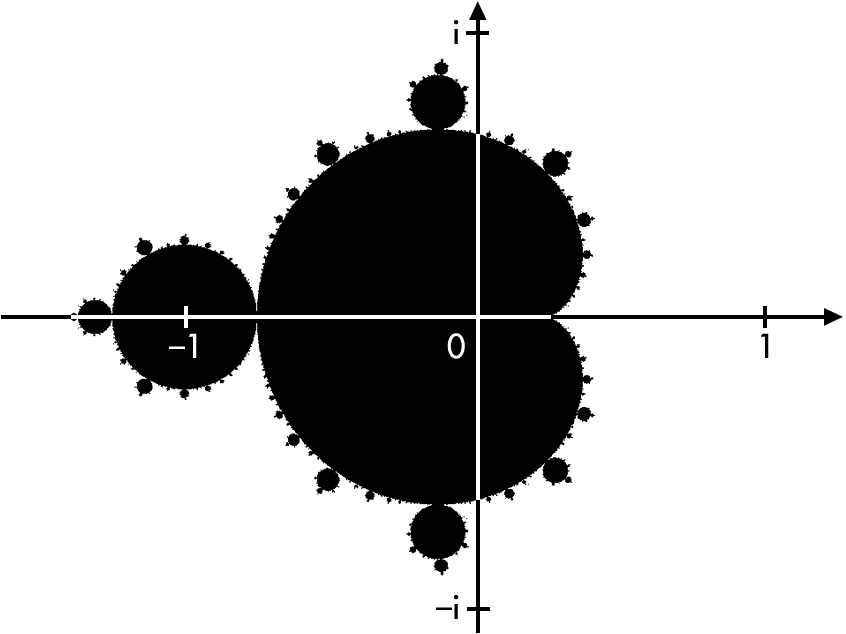
Here are a few examples that follow the formula in this case for C=1 (Not part of mandelbrot set):
zn+1 = zn^2 + c
1 = 0^2 + 1
2 = 1^2 + 1
5 = 4^2 + 1
26 = 5^2 + 1
To form a complex shape like the mandelbrot set, hundreds of thousands and even millions of calculations like the above must be performed to get a detailed image. The more calculations using the formula, the more detailed the Fractal shape will become. Computers significantly improved the ability to explore Fractal equations because of how fast computers can calculate large and complex math equations.


